A note from Andy: Ron is a high school intern for us. I’ve known him for several years through the robotics team that I mentor. He’s been the programmer for the team. Here, he gets to share a thing that he did that made autonomous driving of the robot much, much easier.

During the past several years, I have been a part of FIRST Tech Challenge, a middle school through high school robotics program. Each year a new game is released that is played on a 12ft X 12ft playing field. Each team builds a robot to complete the various game tasks. The game starts off with a 30 second autonomous (computer controlled) period followed by a 2 minute driver-controlled (“teleop”) period. This post addresses robot drive control during the autonomous period.

In my experience on the team, autonomous drive was always somewhat difficult to get to work right. It was normally accomplished by something like driving X encoder counts to the left, turn Y degrees, then drive Z encoder counts to the right. Any additional movements were added on top of this kind of initial drive. One of the major disadvantages of this method is that when you adjust any one linear drive or turn, you then have to change all of the following drives that are built on top of the drive you adjusted. We began to think, “wouldn’t it be nice if we could just tell the robot ‘go to (X, Y)’ and then it went there all on its own.” This all seemed impossible, but this past year, our dreams (which might be the same as yours) began to come true.

In years past, FIRST (the head organization) had implemented Vuforia in its SDK. The SDK is basic software we are required to use. Vuforia is machine vision for smartphones that enables localization. Vuforia would identify vision targets on the field walls and then report back the location of the camera relative to the target. The location of the robot could then be determined with some matrix math.

However, we found that Vuforia was only able to get an accurate reading on the targets while the camera was within 48 inches of the target. See the image below to get an idea of how much of the field is excluded from useful Vuforia position information.
Since we are frequently well out of range of the vision targets, Vuforia was not the solution to our problem.

Then, we considered using the drive wheel encoders. Based off of the robot’s initial position we would track the encoder deltas and compute the live location of the robot. Our initial concern with this idea was that the wheels would slip and cause the robot to lose knowledge of its location. This would make the use of encoders for localization useless. Thus, our dreams remained crushed like mashed potatoes. But when all hope seemed lost, in came an inspiration: we could use the encoders to track the location, and then calibrate that location when we get a Vuforia reading. With this in mind, we began work on encoder based localization software, which we call a dead reckoner.

The initial step in development was to record the encoder values from a drive around the field. We would then be able to use this data for the development of our math, checking it against a video of the drive.

This is the video of the drive that goes with that initial data collection:

For scale in the video, note that the tiles on the field are 24 inches square, shown by the jagged edged grid.

After much hard work, we developed an algorithm that uses the encoder deltas to track the robot’s location. This is a plot (with a scale in inches) of the computed location of the robot over that drive:

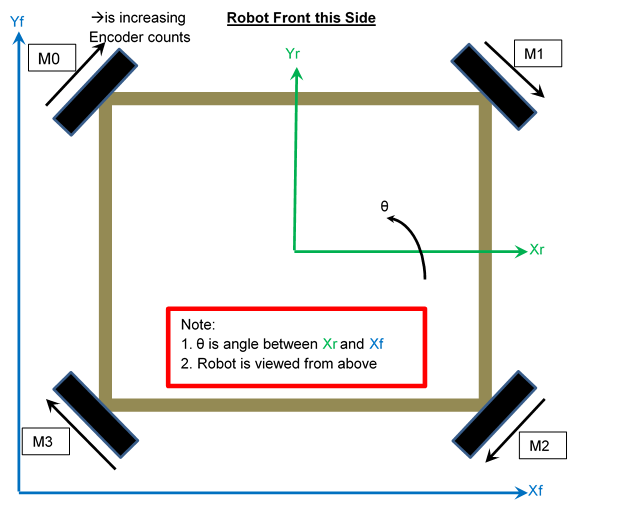
Before we describe the algorithm, we need to define a coordinate system for the robot and the field and the robot. Here is a diagram of the robot and its wheel locations and a picture so that you can see where the wheels are located and how we’ve defined axes for the robot and the field.

The math for the dead reckoner is implemented within a Java method that is called, with new encoder values, on every pass through the opmode’s loop() method. The final math for the system using a four-wheel omni drive is as follows:

//Compute change in encoder positions
delt_m0 = wheel0Pos - lastM0;
delt_m1 = wheel1Pos - lastM1;
delt_m2 = wheel2Pos - lastM2;
delt_m3 = wheel3Pos - lastM3;

//Compute displacements for each wheel
displ_m0 = delt_m0 * wheelDisplacePerEncoderCount;
displ_m1 = delt_m1 * wheelDisplacePerEncoderCount;
displ_m2 = delt_m2 * wheelDisplacePerEncoderCount;
displ_m3 = delt_m3 * wheelDisplacePerEncoderCount;

//Compute the average displacement in order to untangle rotation from displacement
displ_average = (displ_m0 + displ_m1 + displ_m2 + displ_m3) / 4.0;

//Compute the component of the wheel displacements that yield robot displacement
dev_m0 = displ_m0 - displ_average;
dev_m1 = displ_m1 - displ_average;
dev_m2 = displ_m2 - displ_average;
dev_m3 = displ_m3 - displ_average;

//Compute the displacement of the holonomic drive, in robot reference frame
delt_Xr = (dev_m0 + dev_m1 - dev_m2 - dev_m3) / twoSqrtTwo; 
delt_Yr = (dev_m0 - dev_m1 - dev_m2 + dev_m3) / twoSqrtTwo;

//Move this holonomic displacement from robot to field frame of reference
robotTheta = IMU_ThetaRAD;
sinTheta = sin(robotTheta);
cosTheta = cos(robotTheta);
delt_Xf = delt_Xr * cosTheta - delt_Yr * sinTheta;
delt_Yf = delt_Yr * cosTheta + delt_Xr * sinTheta;

//Update the position
X = lastX + delt_Xf;
Y = lastY + delt_Yf;
Theta = robotTheta;
lastM0 = wheel0Pos;
lastM1 = wheel1Pos;
lastM2 = wheel2Pos;
lastM3 = wheel3Pos;

After we got the initial math working, we continued with our testing. All seemed to work well until we turned the robot. After turning the robot, the robot’s heading, Θ, wasn’t calculated correctly. Thus, when we drove after turning the robot, the dead reckoner though we were going in one direction instead of the actual direction we were driving in. We then recorded dead reckoner and IMU data from a simple 360-degree turn, without any driving forward. We found that as we approached 180 degrees, the error between the reckoner and the IMU grew as large as 16 degrees.

After searching through the code, we were unable to find a solution. In order to make the reckoner useful for completion, we band-aided the system by using the IMU heading. This solved our problems for the most part. Everything worked properly except when you turned and drove at the same time. It appears that the issue is due to a time delay between the IMU and encoder values.

After we had finished the Dead Reckoner, we built a robot driver that uses the robot’s position to drive the robot to a specific location on the field. If you string together multiple points, you can accomplish a fully autonomous drive around the field as seen in this video:

The accuracy of this system, was roughly within 1 inch.

With this type of robot drive, programming autonomous drives is almost effortless. Now all you say is “go there”, and it goes there. No more telling the robot “go this far then that far” and then reprogramming that all over again when you need to adjust distances. For example, the above drive around the entire field was programmed in less than 2 minutes; under the traditional method, it would take 10 minutes to do it right. If any adjustments to your distances are needed the traditional method could take as long as 20 minutes.

Future fixes and wish list items for this code include:

Find the source of the angular rotation error so that we can use the encoders without requiring IMU (we should be able to do this)
Determine if there is a time-delay between IMU and wheel encoders reading so that the IMU can be used as a comparison to help detect errors in the wheel motion.

Blog

Robot Localization -- Dead Reckoning in First Tech Challenge (FTC)

Bridge Fusion Systems LLC